Robbins [1] considered the following family of problems:
\(
\begin{array}{ll}
Min \displaystyle \frac{1}{2} \int_0^T \alpha y(t) + \frac{1}{2} u(t)^2 \quad dt;
\quad {y}^{(3)}(t) = u(t); \;\; y(t) \geq 0.
\end{array}
\)
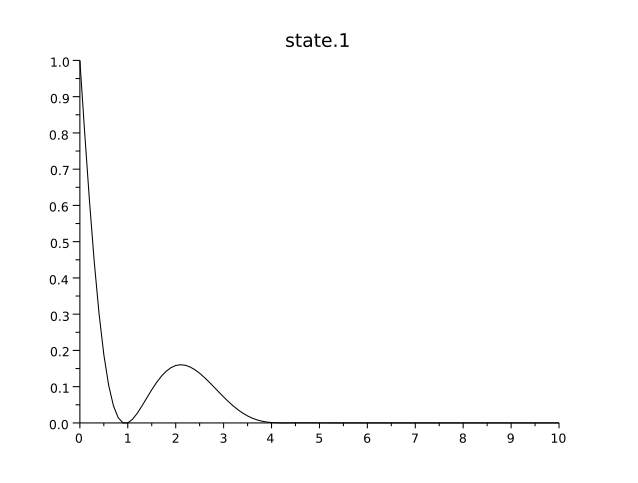
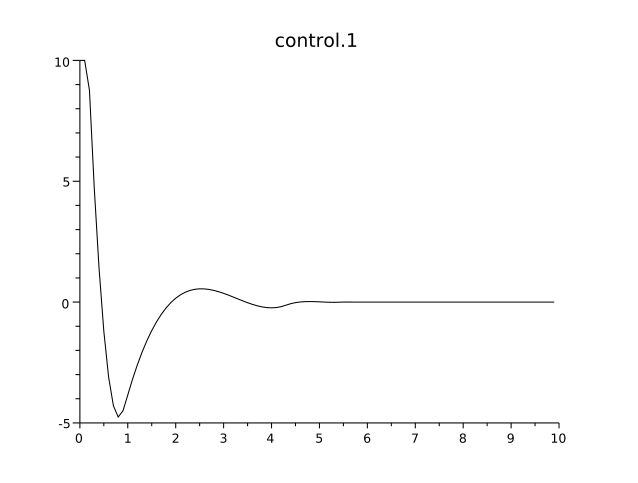
It has been proved by Robbins [1] that, for appropriate initial conditions, the exact solution has infinitely many isolated contact points, such that the length of unconstrained arcs decreases geometrically. Detailed computations can be found in [2]. Therefore the isolated contact points have an accumulation point; the latter is followed by the trivial singular arc \(u=0\), \(y=0\). It is not easy to reproduce numerically this behaviour, since the unconstrained arcs rapidly become too small to be captured by a given time discretization. We display in Figure1 the value of the first state component and of the control.
Numerical simulations: problem state_constraint_3
Discretization: Runge-Kutta 4 with 100 steps.
We take here \(\alpha=3\), \(T=10\), \(y(0)=(1,-2,0)\).
Figure 1
References:
[1] H. M. Robbins. Junction phenomena for optimal control with state-variable inequality constraints of third order. J. of Optimization Theory and Applications, 31:85–99, 1980.