Inverted pendulum

Inverted pendulum

The inverted pendulum has Lagrangian $L=\frac{1}{2} m \dot \theta^2 - g \cos\theta$ , and equation $m\ddot \theta = g \sin\theta$ where $\theta$ is the angle to the vertical. Alternatively, let $(x,y)$ be the Cartesian coordinates of the position of the pendulum, subject to the constraint $G(x,y)=\frac{1}{2}(x^2+y^2-1) = 0$ .
The Lagrangian is then

$L= \frac{1}{2}(\dot x^2 + \dot y^2) + m g y + \frac{1}{2}\lambda(x^2+y^2-1),$

and the mechanical equations are

$m \ddot x = \lambda x + u, \quad m \ddot y = \lambda y - m g.$

where we have set an horizontal force as the control $u$ .
We want to minimize the objective

$Min \int_0^T x^2(t) + (y(t)-1)^2 + u^2(t) \quad dt$

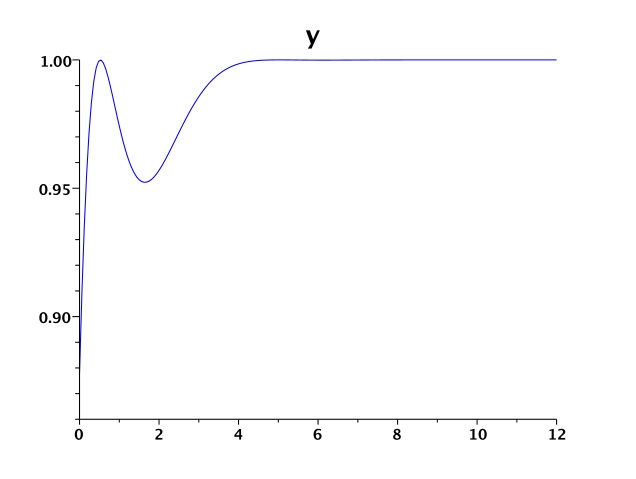
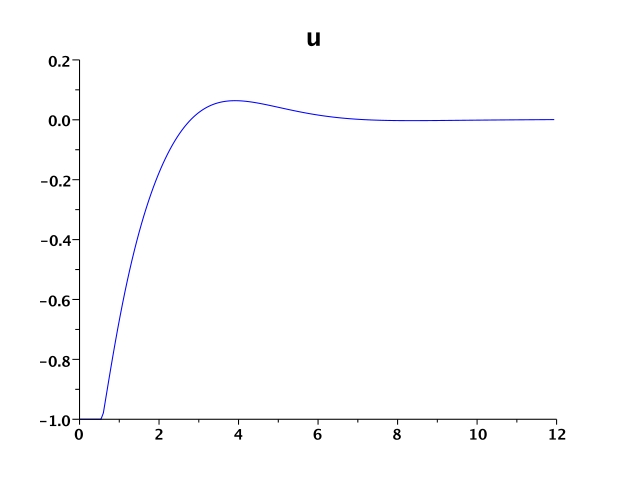
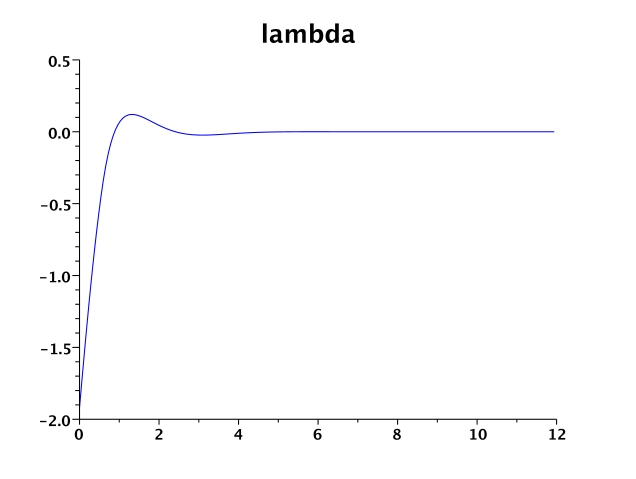
Figure 1 shows the states $x,y$ , the control $u$ and multiplier $\lambda$ .

Numerical simulations:
Discretization: Runge Kutta 4 with 400 steps.
We take here $T=12$ , $m=1$ and $g=1$ .
The final conditions are

$\begin{array}{lll} x(T)=0 &,& y(T)=1\\ \dot x(T)=0 &,&\dot y(T)=0 \end{array}$

The initial conditions are

$\begin{array}{lll} x(0)= -0.4794255 &,& y(0)=0.8775826\\ \dot x(0)= 1.0530991 &,& \dot y(0)= 0.5753106 \end{array}$

Links

Contact