Harvest

We study here the delay problem studied in [1] and [2], originating from [4]. The aim is to find the optimal harvesting of a renewable ressource whose growth follows a logistic function. Denoting $x$ the biomass of population and $u$ the harvesting effort, the optimal control problem is stated as

$\left \lbrace \begin{array}{l} Min\ \int_0^T e^{-\beta t}(C_E\frac{u(t)^3}{x(t)} -pu(t))dt +0.1 T^2\\ \dot x = a x(t) (1 - \frac{x(t-h)}{b}) - u(t)\\ x(t) = 2\ \forall t \in [-h,0] \quad,\quad x(t) \ge 2\ \forall t \in [0,T]\\ u(t) \ge 0\ \forall t \in [0,T]\\ T\ free. \end{array} \right.$

with the harvesting cost $C_E=0.2$ , the growth rates $a=3,b=5$ , the discount rate $\beta=0.05$ and market price $p=2$ , and the growth delay $h=0.5$ . Bocop can handle the delayed term $x(t-h)$ without having to perform the classical Guinn transformation ([3]), but for a fixed final time only. Therefore we perform a batch of optimizations for $T\in[1,20]$ , and iterate the process for $T\in[11,13]$ to find a better estimate of the optimal time. Batch optimizations indicate an optimal final time $T^*\approx12.24$ with an objective $J^*=-26.15$ .

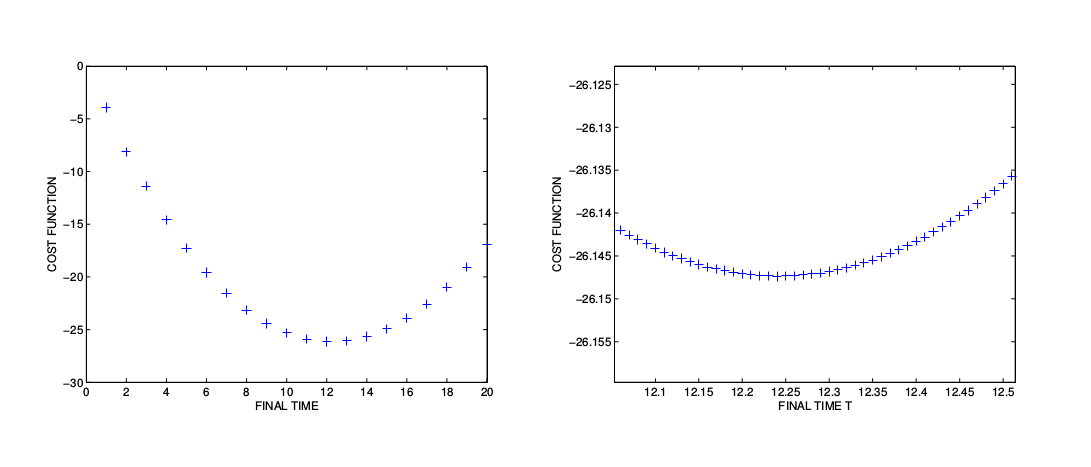
Fig1: Delay problem. Cost function with respect to final time T.

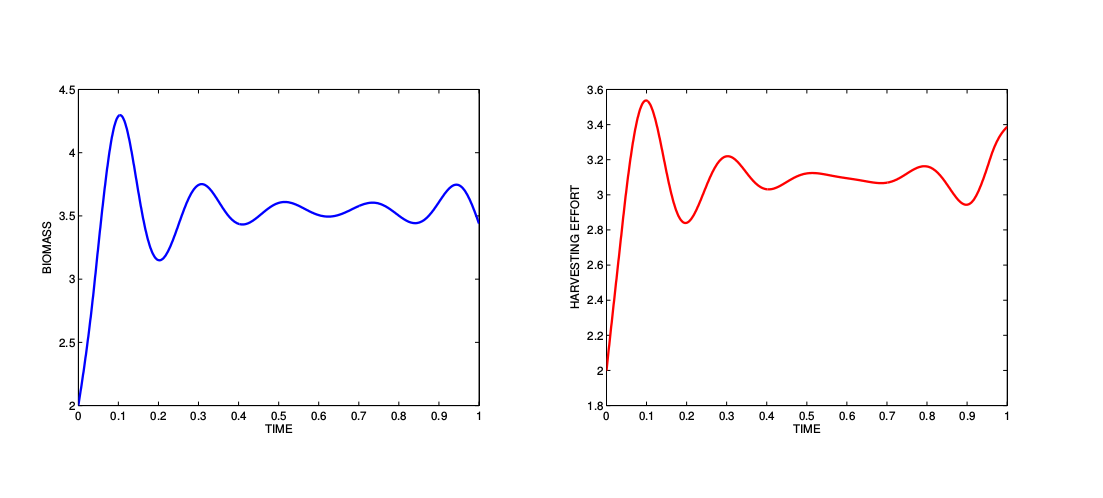
Fig2: Delay problem. Optimal state and control for T = 12.24.

References
[1] A. Boccia, P. Falugi, H. Maurer, and R. Vinter. Free time optimal control problems with time delays. pages 520–525. IEEE, 2013.
[2] L. Goellmann, D. Kern, and H. Maurer. Optimal control problems with delays in state and control variables subject to mixed control-state constraints. Optimal Control Applications and Methods, 30(4):341–365, 2009.
[3] T. Guinn. Reduction of delayed optimal control problems to non-delayed problems. Journal of Optimization Theory and Applications, 18(3):371–377, 1976.
[4] R. May. Stability and Complexity in Model Ecosystems. 1975.

Links

Contact