A simple Goddard problem

Goddard problem

This well-known problem (see for instance [1],[2]) models the ascent of a rocket through the atmosphere, and we restrict here ourselves to vertical (monodimensional) trajectories.
The state variables are the altitude, speed and mass of the rocket during the flight, for a total dimension of 3. The rocket is subject to gravity, thrust and drag forces. The final time is free, and the objective is to reach a certain altitude with a minimal fuel consumption, ie a maximal final mass. All units are renormalized.

$(P_3) \left \lbrace \begin{array}{l} \max \ m(T)\\ \dot r = v\\ \dot v = - \frac{1}{r^2} + \frac{1}{m} (T_{max} u - D(r,v))\\ \dot m = - b u\\ u(\cdot)\in [0,1]\\ r(0) = 1, \ v(0)=0, m(0)=1,\\ r(T) = 1.01\\ D(r(\cdot),v(\cdot)) \le C\\ T\ free \end{array} \right .$

The drag is $D(r,v):=Av^2\rho(r)$ , with the volumic mass is $\rho(r) := exp(-k*(r-r0))$ .
We use the parameters $b=7, T_{max}=3.5, A=310, k=500, r0=1$ .

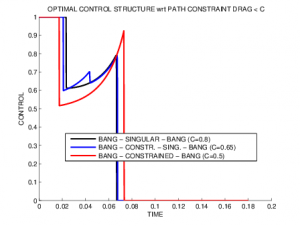
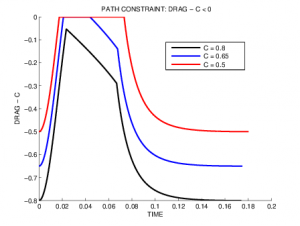
The Hamiltonian is an affine function of the control, so singular arcs may occur. We consider here a path constraint limiting the value of the drag effect: $D(r,v) \le C$ . We see that depending on the value of C, the control structure changes. In the unconstrained case, the optimal trajectory presents a singular arc with a non-maximal thrust. When C is set under the maximal value attained by the drag in the unconstrained case, a constrained arc appears. If C is small enough, the singular arc is completely replaced by the constrained arc.

Numerical simulations:
Discretization: Gauss 4th order with 1000 steps.
Depending on the value of C, the optimal control structure changes from Bang-Singular-Bang to Bang-Constrained-Bang.

References

[1] R.H. Goddard. A Method of Reaching Extreme Altitudes, volume 71(2) of Smithsonian Miscellaneous Collections. Smithsonian institution, City of Washington, 1919.

[2] H. Seywald and E.M. Cliff. Goddard problem in presence of a dynamic pressure limit. Journal of Guidance, Control, and Dynamics, 16(4):776–781, 1993.

Links

Contact