Fuller problem

Fuller problem

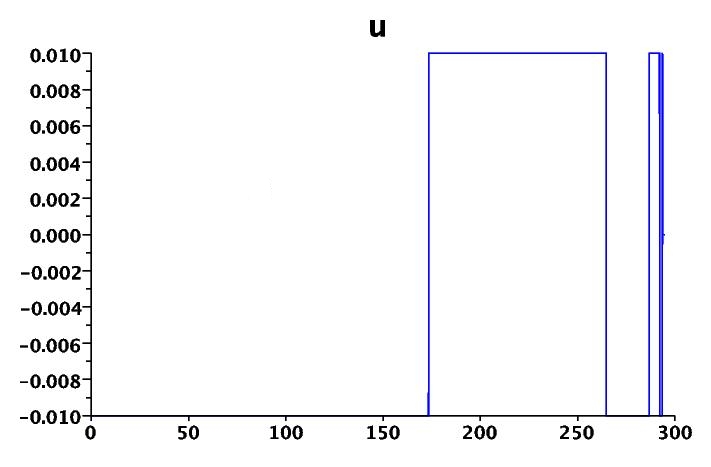
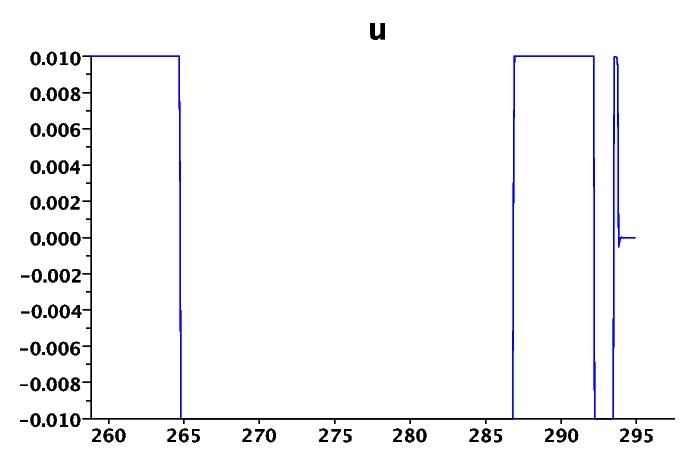
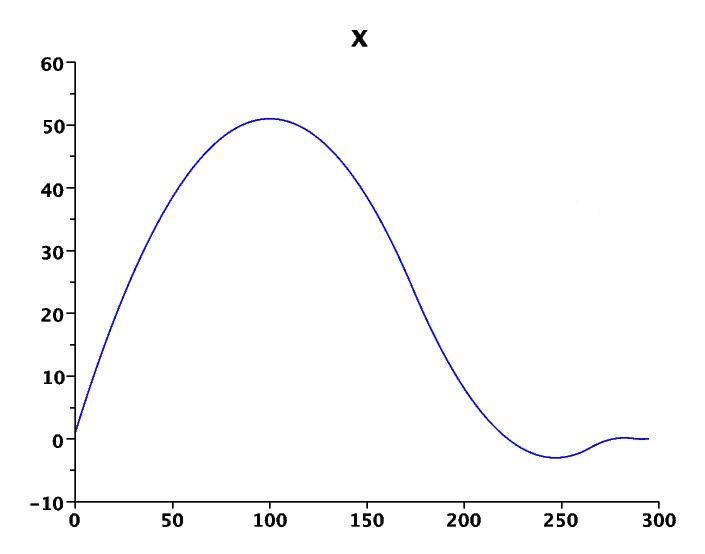
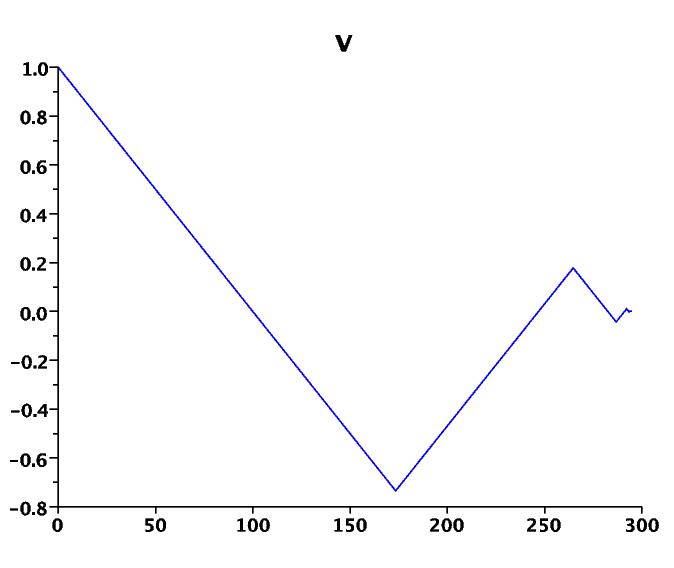
Here is a very classical example of a chattering phenomenon [1]:

$Min \int_0^T x^2(t) dt; \quad \ddot x(t) = u(t) \in [-1,1].$
The solution is, for large enough T, bang-bang (i.e., with values alternately $\pm 1$ ), the switching times geometrically converging to a value $\tau>0$ , and then the (trivial) singular arc $x=0$ and $u=0$ . These switches are not easy to reproduce numerically. We display in figure 1 the control, with a zoom on the entry point of the singular arc.

Numerical simulations: problem fuller
Discretization: Gauss II with 1000 steps.
We take there $T=3.5$ , $x(0)=0, \dot x(0)=1$ , $x(T)=\dot x(T)=0$ and $u(t) \in [-10^{-2},10^{-2}]$ .

Figure 1: Fuller problem: chattering control (with zoom); x and v.
_________________________________________________________________________
References
A.T. Fuller. Study of an optimum non-linear control system. J. of Electronics and Control, 15:63-71, 1963

Links

Contact