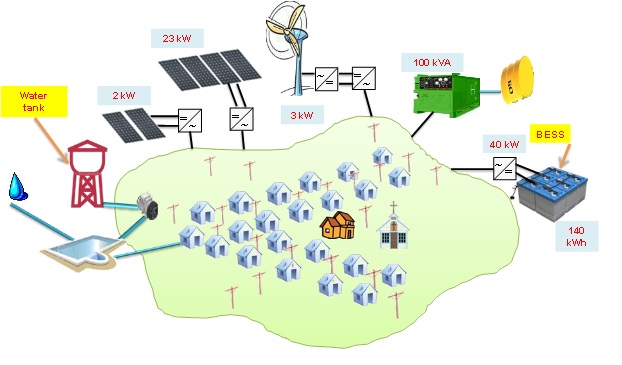
Energy management for an electric microgrid

We present here a microgrid problem introduced and solved by MILP techniques in [1], later studied in [2] with direct and Hamilton-Jacobi-Bellman methods. In the context of an isolated village in the Chilean mountains, we consider a microgrid comprised of a diesel generator, photo-voltaic panels and a battery energy storage system (BESS). The aim is to satisfy the energy demand (power load) from the villagers at all times, while minimizing the overall diesel consumption. One of the difficulties is that the diesel generator has a turn-on cost, thus we have to keep track of its on/off state over time. This problem falls in the class of switched systems and can be solved with a dynamic programming approach.

We consider a fixed horizon T = 48 hours. For t ∈ [0, T], we denote by PS(t) the solar power from the photovoltaic panels, PD(t) the diesel generator power and PL(t) the electricity load.

Dynamics. The state of charge SOC(t) of the BESS evolves according to

$\dot{SOC}(t) = \frac{1}{Q_B}\left(P_I(t) \rho_I- P_O(t)/ \rho_O\right) = \frac{1}{\tilde{Q}_B}\left(P_I(t) \tilde{\rho}- P_O(t)\right)$

where Q_B is the maximum capacity of the battery, $P_I, P_O > 0$ are the input and output power of the BESS, and $\rho_I, \rho_o$ are the efficiency ratios for the charge and discharge processes, assumed constant. We introduce the slack variable $P_{slack}$ that represents the excess power $(P_{slack} <0)$ , which has to be shed, or the missing power in the microgrid $(P_{slack} >0)$ , which turns into unmet demand. The addition of this variable ensures the mathematical feasibility of the problem.

Cost function.We model the fuel consumption of the diesel generator by

$\int_0^T K P_D(t)^{0.9} dt, \quad K=0.471.$

The fuel consumption curve is strictly concave and was extrapolated from the datasheet provided by the diesel generator manufacturer as in [1]. Note that turning the diesel generator on adds a fixed instantaneous consumption of 2l. Total cost is the sum of the diesel cost and unserved energy cost $C_{US} P_{slack}^+$ , with $C_{US}=1000CLP$ and the unit price for diesel $C_D=500 CLP$ (Chilean Pesos).

Constraints. For physical reasons, the system is subject to the following constraints at every time $t\in [0,T].$ These include the bounds for the battery state of charge, diesel generator power output, and discharge charge limits for the BESS

$\left \lbrace \begin{array}{l} SOC(t) \in [0.2,1],P_D(t)\in\{0\} \cup [5,120],P_O(t)\in[0,40], \\ P_{I}(t,P_D(t),P_{slack})\in [0,13.2]\ if\ SOC(t) <0.9, \\ P_I(t,P_D(t),P_{slack})\leq 1320(1-SOC(t))^2 \ otherwise. \end{array} \right.$

Moreover, the power equilibrium must hold at all times and can be used to eliminate some of the variables:

$P_D + P_O + P_S + P_{slack} - P_L - P_I = 0.$

External data. We choose two test cases of a 48h time frame in winter and summer. The power load $P_L$ and solar power $P_S$ are shown below.

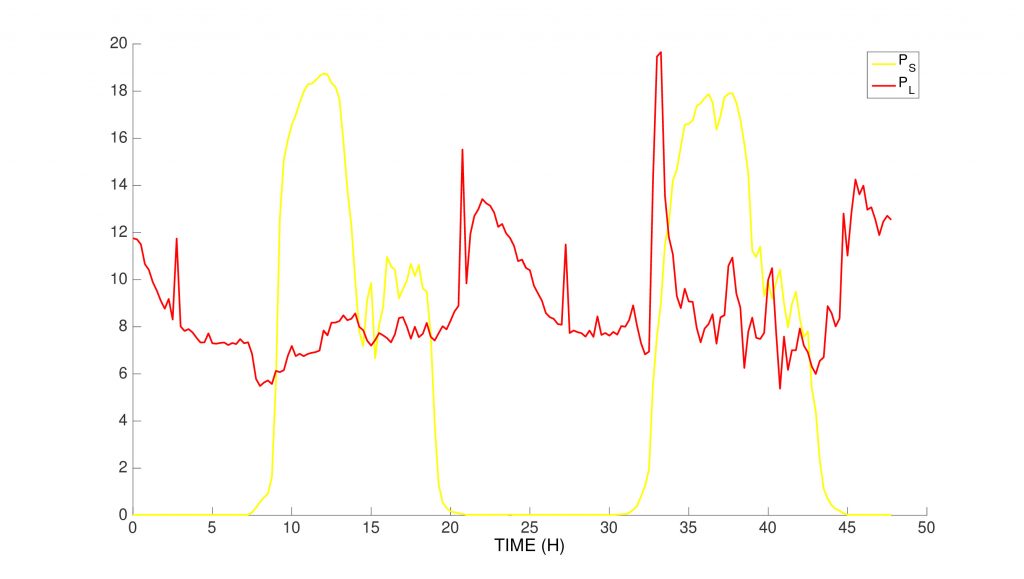
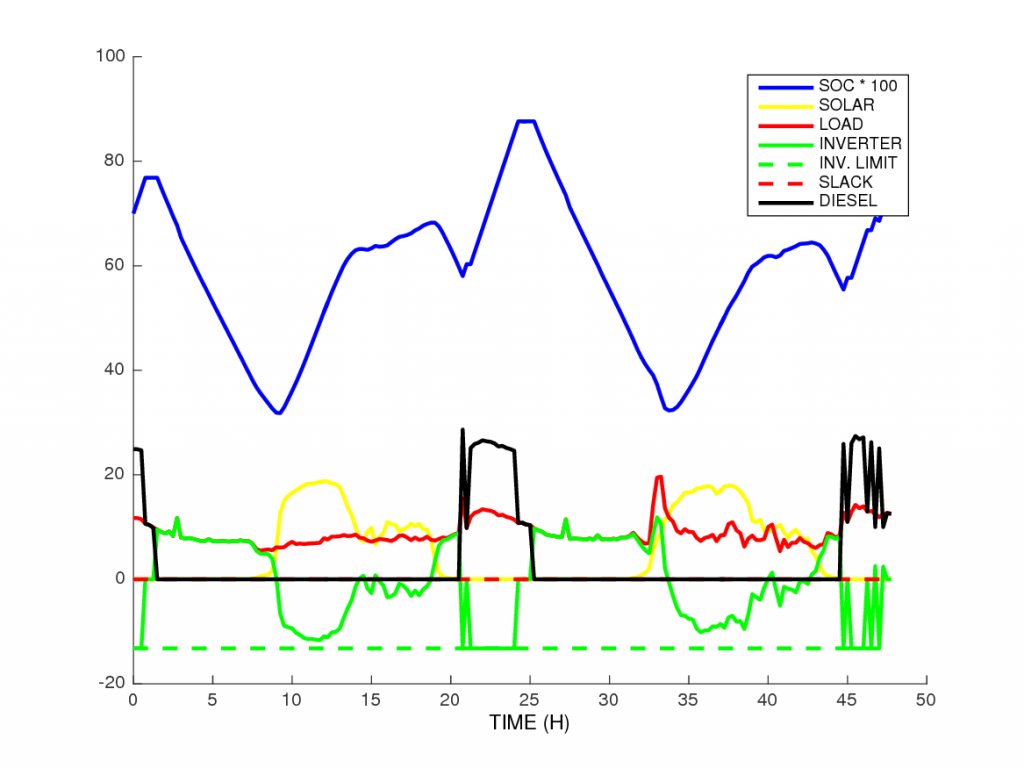
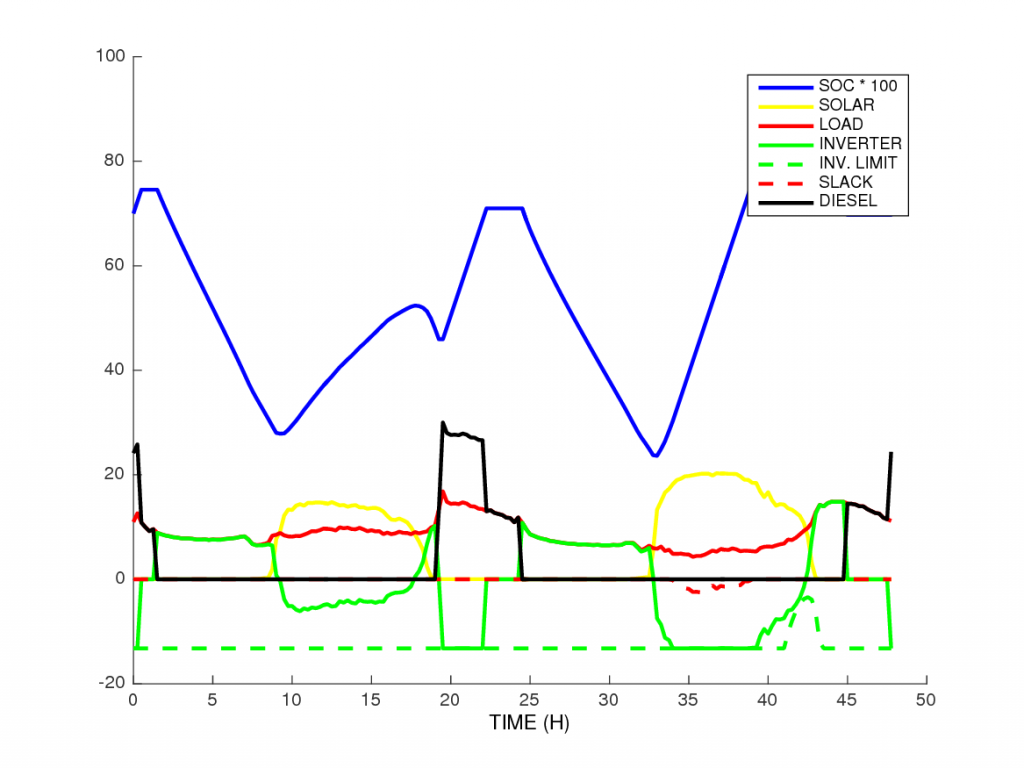
summer data

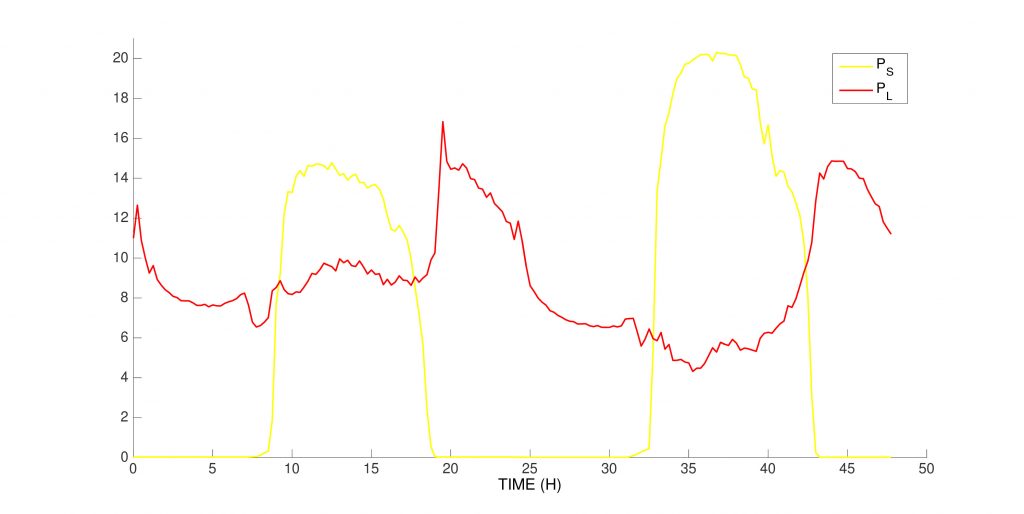
winter data

The ‘PMP trick’.This problem can be solved directly by BocopHJB using a basic control discretization for $P_D$ and $P_{slack}$ . However, in this particular case, we are able to exploit the properties of the problem to improve the method. If $\bar{u}$ is the optimal control, denote by $\bar{x}$ the optimal state and $\bar{p}$ the costate associated to the dynamics constraint $\dot{x}(t)= F(t,u(t))$ . Defining the Hamiltonian $H(u,p,t) := pF(u,t)+\ell(u)$ the Pontryagin’s Maximum Principle (PMP) says that for all $t\in [0,T]$ we have

$H(\bar{u}(t),\bar{p}(t),t) \leq\ H(v,\bar{p}(t),t)\ for\ all\ v\in U_{\bar{x}(t)}.$

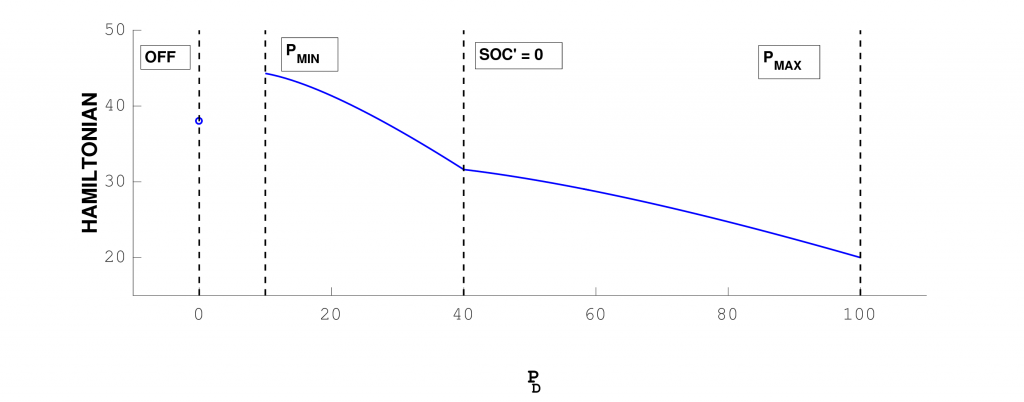
Since the dynamics is continuous and piecewise affine, the Hamiltonian is the sum of a continuous, piecewise affine and of a continuous strictly concave functions, and therefore is continuous, piecewise strictly concave. Therefore it can attain its minimum only at one of the extreme points of the pieces. Taking into account the constraints, we have at most five possible optimal controls, as illustrated below. Moreover, the values of these controls can be computed explicitly, since they do not depend on $\bar{p}$ (which is not true in general). Therefore, instead of the usual control discretization we only test these controls, gaining both in speed and precision.

So:
– if the Diesel is off (mode 0), we simply take $P_D=0$ .
– if the Diesel is on (mode 1), we test the five cases:

$P_D=5$ (minimum power)
$P_D=120$ (maximum power)
$P_D$ such that $\dot{SOC}=0$ (battery unused)
$P_D$ such that $P_i = P_i^{max}(SOC)$ (maximal charge)
$P_D$ such that $P_0=40$ (maximal discharge)

We present the results of the optimization for the two test cases. The Solar Power fills the demand, with any excess power used to charge the battery. The Diesel is always off when solar power is available, and is switched on once a day during the evening peak in demand. The Diesel output is often greater than power demand: it is also used to charge the battery. The battery fills the gaps between production and demand especially at night.

summer data

winter data

Other formulations. We can also solve the problem using a manual control discretization for $P_D \in {0} \cup [6,120].$ Finally, given the small number of admissible controls, we can actually model each of them with modes and remove the control $P_D$ altogether. The solutions obtained by the different formulations are quite close.

References
[1] R. Palma-Behnke, C. Benavides, F. Lanas, B. Severino, L. Reyes, J. Llanos, and D. Sez. A microgrid energy management system based on the rolling horizon strategy. IEEE Transactions on Smart Grid, 4(2):996–1006, 2013.
[2] Benjamin Heymann, J. Frédéric Bonnans, Pierre Martinon, Francisco J. Silva, Fernando Lanas, and Guillermo Jiménez-Estévez. Continuous optimal control approaches to microgrid energy management. Energy Systems, 2017. DOI

Links

Contact