The inverted pendulum has Lagrangian \(L=\frac{1}{2} m \dot \theta^2 – g \cos\theta\), and equation \(m\ddot \theta = g \sin\theta\) where \(\theta\) is the angle to the vertical. Alternatively, let \((x,y)\) be the Cartesian coordinates of the position of the pendulum, subject to the constraint \(G(x,y)=\frac{1}{2}(x^2+y^2-1) = 0\).
The Lagrangian is then
\(
L= \frac{1}{2}(\dot x^2 + \dot y^2) + m g y + \frac{1}{2}\lambda(x^2+y^2-1),
\)
and the mechanical equations are
\(
m \ddot x = \lambda x + u, \quad m \ddot y = \lambda y – m g.
\)
where we have set an horizontal force as the control \(u\).
We want to minimize the objective
\(
Min \int_0^T x^2(t) + (y(t)-1)^2 + u^2(t) \quad dt
\)
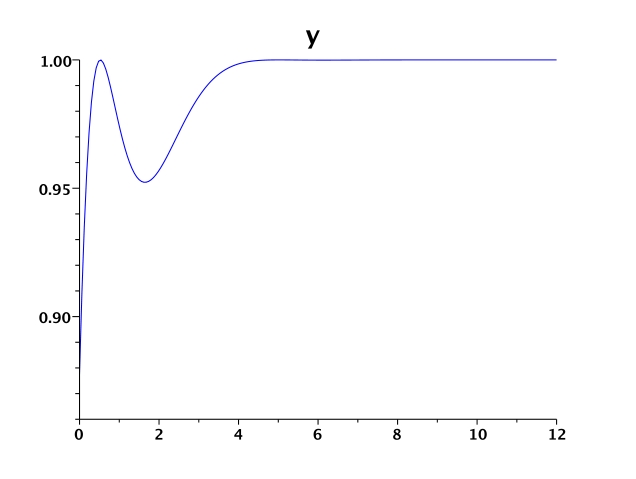
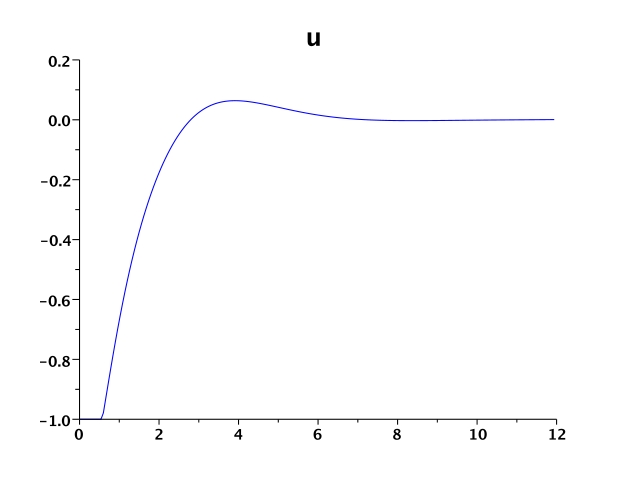
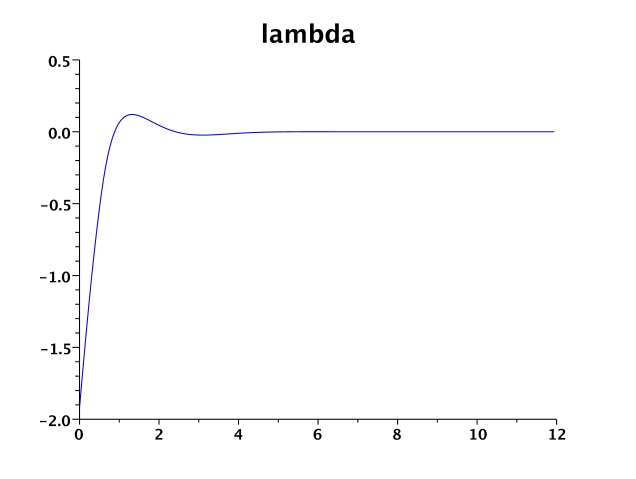
Figure 1 shows the states \(x,y\), the control \(u\) and multiplier \(\lambda\).
Numerical simulations:
Discretization: Runge Kutta 4 with 400 steps.
We take here \(T=12\), \(m=1\) and \(g=1\).
The final conditions are
\(
\begin{array}{lll}
x(T)=0 &,& y(T)=1\\
\dot x(T)=0 &,&\dot y(T)=0
\end{array}
\)
The initial conditions are
\(
\begin{array}{lll}
x(0)= -0.4794255 &,& y(0)=0.8775826\\
\dot x(0)= 1.0530991 &,& \dot y(0)= 0.5753106
\end{array}
\)