We describe here a simple example for the one dimensional heat equation, over the domain \(\Omega=[0,1]\). We set \(Q=\Omega\times [0,T]\), where the final time is fixed. The control \(u(t)\) is either (i) over a part of the domain, with Dirichlet conditions, or (ii) at the boundary by the Neumann condition. So the state equation is in case (i)
\(
\frac{d}{dt} y(x,t)- c_0\ y_{xx}(x,t) = \chi_{[0,a]} c_1\ u(t), \quad (x,t) \in Q,
\)
\(
y(\cdot,0)=y_0(x); \quad y(0,t)=y(1,t) = 0, \quad t\in [0,T],
\)
where \(0<a\leq 1\), and \(\chi_{[0,a]}\) is the characteristic function of \([0,a]\), and in case (ii)
\(
\frac{d}{dt} y(x,t) – c_0\ y_{xx}(x,t) = 0, \quad (x,t) \in Q,
\)
\(
y(\cdot,0) =y_0(x); \quad y_x(0,t)= -c_1 u(t); \quad y_x(1,t) = 0, \quad t\in [0,T].
\)
The cost function is, for \(\gamma\geq 0\) and \(\delta\geq 0\):
\(
\frac{1}{2} \int_Q y(x,t)^2 dx dt + \int_0^T \left( \gamma u(t) + \delta u(t)^2\right) dt.
\)
We discretize in space by standard finite difference approximations.
Numerical simulations: problem heat
As an example, we take 50 space variables, with \(c_0=0.02\), \(c_1=20\), and a final time T=20.
The discretization method is implicit Euler with 200 steps.
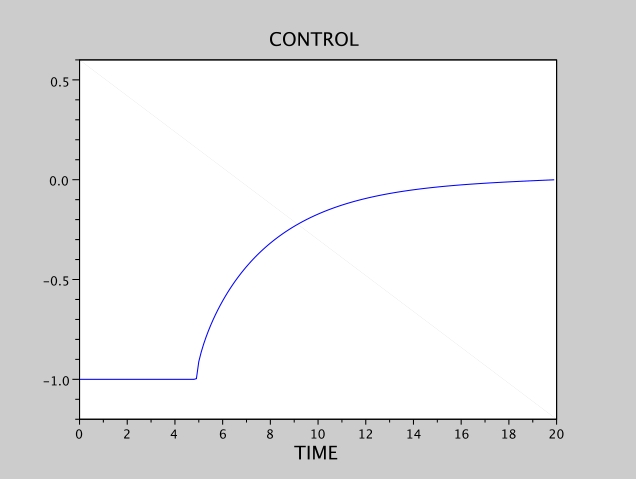
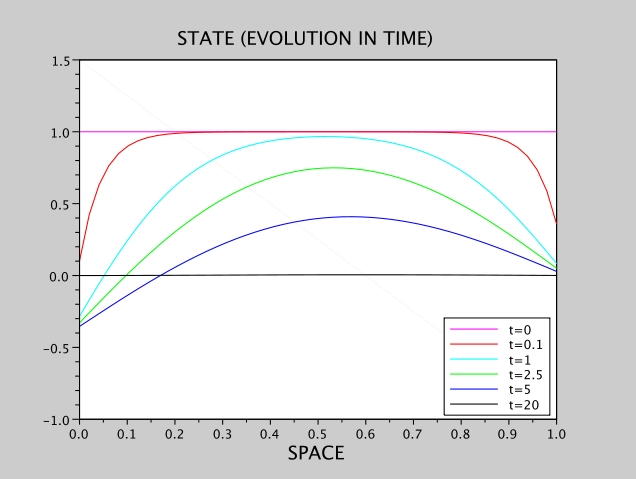
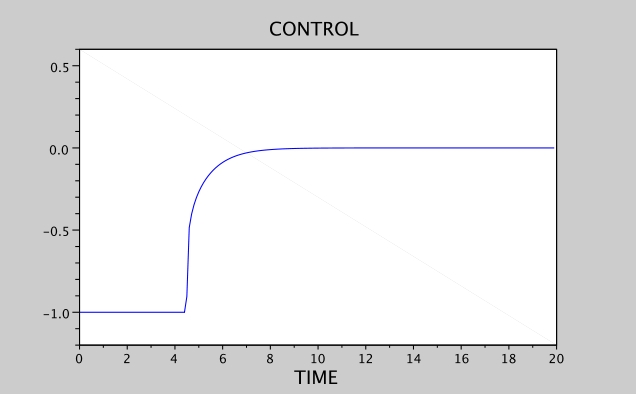
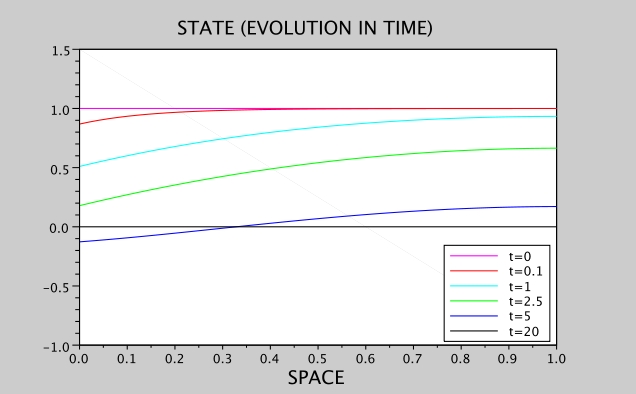
We set here \(\gamma = \delta=0\), which gives a singular arc for the control.
We display on Fig. 1 the results in the case of the Dirichlet boundary condition \((a=0)\).
Fig. 2 shows the Neumann case, this time with \(c_0=0.2\).
We can clearly see the differences between the boundary conditions \(y(1,t)=0\) and \(y_x(1,t)=0\).
Figure 1: Heat equation, Dirichlet condition, \(u(t)\) and \(y(.,t)\).
Figure 2: Heat equation, Neumann condition, \(u(t)\) and \(y(.,t)\).