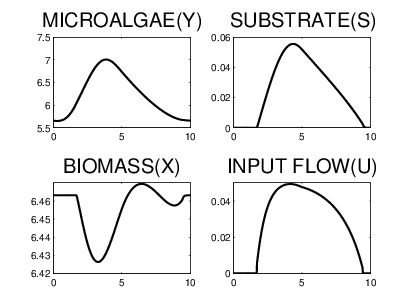Anaerobic digestion of micro-algae for bio-gaz production

Coupling microalgae culture and anaerobic digestion is a promising process to convert solar energy into methane. In [1,2] we consider a dual tank reactor: a first one in which microalgae are cultivated and a second one where the microalgae are converted into biogas. Our first aim is to find an optimal feeding strategy in order to maximize the production of biogas in the second reactor during one day.

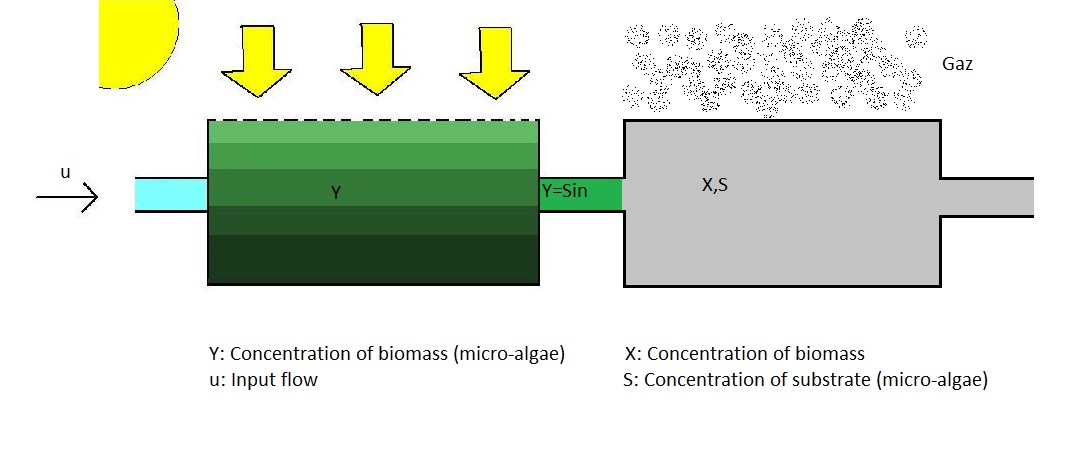The dual-tank bioreactor can be modeled as a 3-dimensional dynamical system. The state variables are the concentration of micro-algae y, biomass x and substrate s. The control variable is the input flow u throughout the whole reactor. The system dynamics is given by
$(*)\left \lbrace \begin{array}{l} \frac{dy}{dt}=\frac{\mu(t)y}{1+y} - ry - uy\\ \frac{ds}{dt}=-\mu_2(s)x + u\beta(\gamma y-s)\\ \frac{dx}{dt}=(\mu_2(s)-u\beta)x \end{array} \right .$
where $\mu$ is the light model, $\mu_2(s)=\mu_2^m \frac{ s}{ K_s + s}$ the growth function in reactor 2 (Monod), and $\beta$ the volume ratio between the two tanks.

The optimal control problem is written as
$(OCP) \left \lbrace \begin{array}{l} Max \frac{1}{\beta+c} \int_0^{t_f} \mu_2(s(t)) x(t) dt\\ \frac{d}{dt}(y,s,x) = f(t,y,s,x,u) \ (*)\\ u \in [0,1]\\ (y(0),s(0),x(0)) \in Z_0\\ (y(t_t),s(t_f),x(t_f)) = (y(0),s(0),x(0)) \quad (optional) \end{array} \right .$

The periodic optimization over 1 day (T=10) gives the optimal solution

Algae concentration increases during the first half of period ie day, then decreases at night. Biomass concentration in the second tank is almost constant. Here the control structure is Bang(0) – Singular – Bang(0), which is consistent with the Hamiltonian being linear in the control.

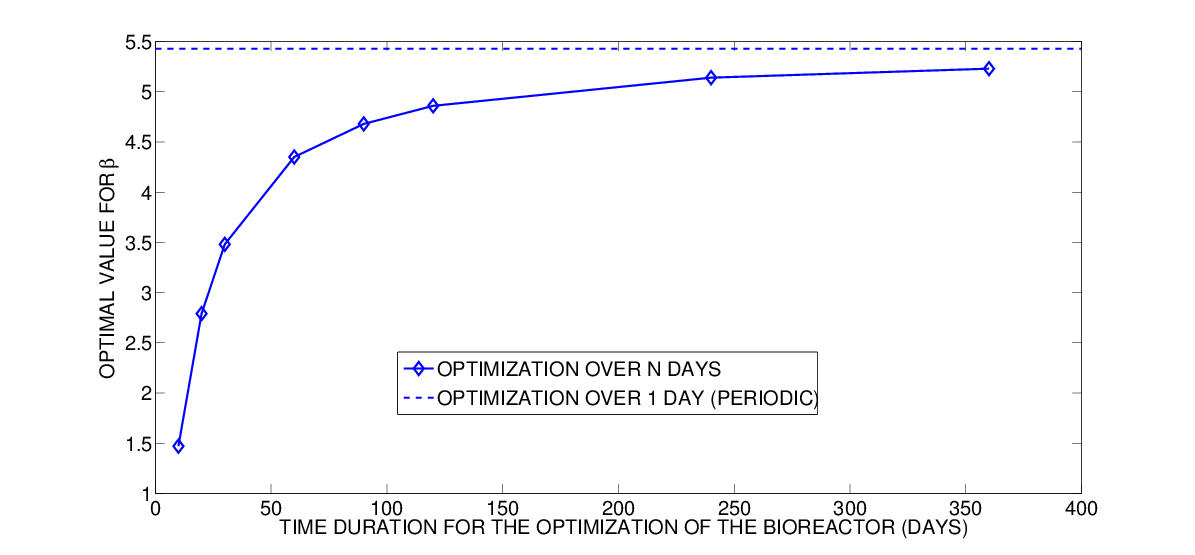
We can also solve the same problem while also optimizing the volume ratio $\beta$ . It turns out the optimal ratio $\beta^*$ seems to depend on the optimization horizon, with an asymptotic value corresponding to the periodic 1-day optimization.

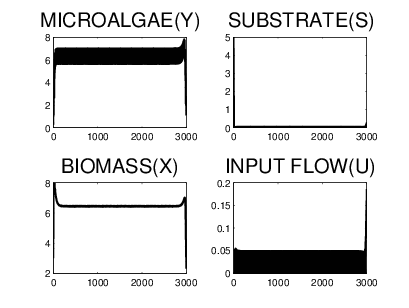
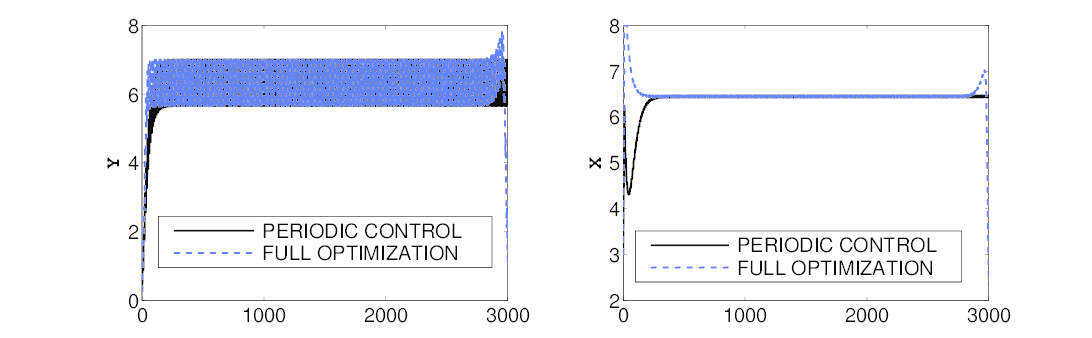
Simulations over a larger time period indicate that the optimal long-term strategy consists in three phases, see below for 30 and 300 days. First we observe an initial phase of growth, starting from the initial conditions to reach some optimal concentrations levels. Then for almost the whole time interval we see a sequence of identical, optimal 1-day periodic cycles. Finally there is a wash-out phenomenon at the end of the time frame, which is more a perturbation.

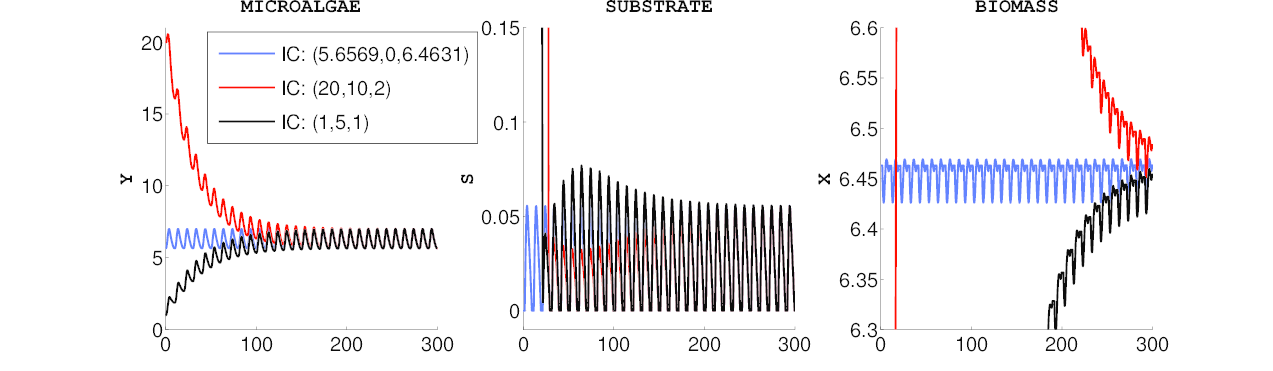
Finally, we also illustrate an attraction property of the dynamical system, established in [2]. We now set the control as the optimal solution from the 1-day periodic problem, and simulate the evolution of the system from different initial conditions. Simulations confirm this fixed sequence of controls drives the system to an optimal mode, after which the trajectory becomes periodic.

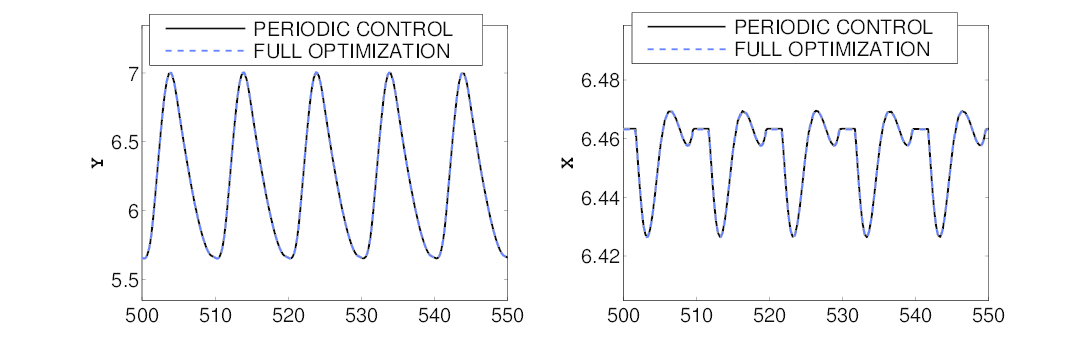
We can check that these periodic 1-day cycles are identical to the ones obtained when performing the full optimization (with free control).

References

[1] T. Bayen, F. Mairet, P. Martinon, and M. Sebbah. Optimizing the anaerobic digestion of microalgae in a coupled process. In 13th European Control Conference, Zurich, Switzerland, 2013.

[2] T. Bayen, F. Mairet, P. Martinon, and M. Sebbah. Analysis of a periodic optimal control problem connected to microalgae anaerobic digestion. Optimal Control Applications and Methods, 2014.

Links

Contact